Acuario

《Redis深度历险》学习笔记：HyperLogLog&布隆过滤器

 学习笔记/Redis  1811  4 分钟

HyperLogLog

  • 通常用来统计一个集合中不重复的元素个数的方法叫做基数计数(cardinality counting)。（eg. 统计页面 UV）
  • HyperLogLog 是 Redis 的高级数据结构，用来解决使用 set 结构进行基数计数时占用空间过大的问题。
  • HyperLogLog 统计的标准误差为 0.81%
  • HyperLogLog 结构的发明人是 Philippe Flajolet，故 HyperLogLog 命令以其名字首字母缩写 pf 开头：
    • pfadd：向键内增加元素，并去重。
    • pfcount：统计键内元素数量。
    • pfmerge：将多个 pf 计数值累加在一起形成一个新的 pf 值。适用于合并相似统计项的数值，即 A+B。
    127.0.0.1:6379> pfadd codehole user1
(integer) 1
127.0.0.1:6379> pfadd codehole user2
(integer) 1
127.0.0.1:6379> pfadd codehole user1
(integer) 0
127.0.0.1:6379> pfcount codehole
(integer) 2
  • HyperLogLog 计数较小时，采用稀疏矩阵存储，空间占用很小，计数超过了阈值时转变成稠密矩阵，占用 12KB 的空间。数据量大时性价比明显优于 set 结构。
  • 一个 pf 项占用内存空间 12KB。
  • HyperLogLog 不储存元素本身，不能像 set 那样返回输入的元素。

原理

  • HyperLogLog 是个神奇的算法，它的精髓有 2 点：

    • 恰当的哈希算法对数据的处理可以使数据分布均匀。这一点类似于投足够多次硬币，某一面朝上的概率能够均匀分布在 50% 附近（也就是概率论中的伯努利分布）
    • 对于一个乱序集合，如果元素的哈希值末尾出现的 0 的个数记为 k，那么观察所有元素的 k 值，其中最大值 K 与集合内元素的总数量 N 有相关性：N = 2^K。
      eg. 有 1-37600 的数字随机排列，取出一些数字来进行哈希计算，找出二进制值末尾出现的 0 的最大的个数，发现 K=15 —— 2^15 = 32768

  • 上面还是有点抽象，为什么末尾 0 的个数可以与集合内元素总数相关，想了很久才有了一点眉目，干脆用这个不恰当的栗子来理解好了：

    • 假如有一个骰子，如何通过实验来获知这个骰子上有几种不同的图案？
      其实方法很简单，只需要每投一次就记录一下图案，投足够多次，就可以知道每种图案出现的概率，然后大概就能猜出总共有几种图案。
      这有点像通过查看投硬币的结果来猜测硬币有 2 面而不是 3 面。
    • HyperLogLog 中的哈希算法对数据的处理，保证了哈希结果是均匀随机的，即保证了「投币」的随机性。

  • 这篇文章描述了算法的基本原理——要统计一个数据集合 values 的不重复元素总数时：

    1. 对元素做哈希计算，获得元素的哈希值 h
    2. 哈希值 h 的前几位当作桶 bucket 的编号 n，其余部分 bucket_hash 放入桶中
    3. 查看桶中的值末尾有几个 0，与记录中的最多末尾 0 标志 max_zeroes 进行比较，并更新 max_zeroes
    4. 遍历 values，对每个元素重复 1-3 步

  • Redis 的 HyperLogLog 算法采用 2^14=16384 个桶进行独立计数（原始算法为 1024 个），每个桶使用 6bit 来保存当前桶低位连续零位的最大长度 max_zeroes（最大可表示 2^6-1=63），所以一个 pf 项占用内存空间 2^14 * 6Kbit = 98Kbit = 12KByte。

布隆过滤器

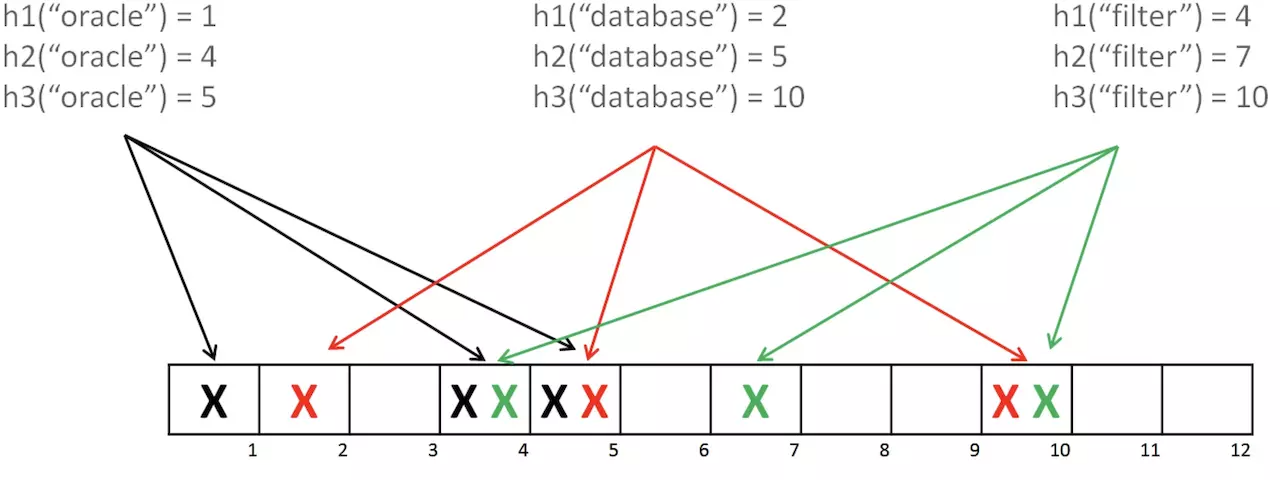
  • 布隆过滤器（Bloom Filter）由布隆于 1970 年提出，它是一个很长的二进制向量和一系列随机映射函数，用于检索一个元素是否在一个集合中。
  • 布隆过滤器原理：
    • 使用 hash 算法对数据进行计算，将其结果对应位置（如1，4，5）设为 1。
    • 验证时对对象进行 hash 计算后查看对应位（如1，4，5）是否都为 1。
    • 受制于空间大小，多个数据的 hash 结果可能重叠，导致验证存在性时的误判。

布隆过滤器

  • 布隆过滤器的空间效率和查询时间都远超一般算法，但存在一定的误识别率和删除困难。
  • 布隆过滤器是一个不够精确的 set 结构，返回 true 时真实结果可能为 false，返回 false 时真实结果一定为 false。
  • 通常使用 3 个基本命令： 
    # 添加元素
127.0.0.1:6379> bf.add codehole user1
(integer) 1

# 批量添加元素
127.0.0.1:6379> bf.madd codehole user2 user3
1) (integer) 1
2) (integer) 1

# 查询元素是否存在
127.0.0.1:6379> bf.exists codehole user1
(integer) 1

# 批量查询元素是否存在
127.0.0.1:6379> bf.mexists codehole user2 user3 user4
1) (integer) 1
2) (integer) 1
3) (integer) 0
  • bf.reserve {key} {error_rate} {capacity} 命令（文档）可以显式创建布隆过滤器（重复创建时会报错），该命令有 3 个参数：
    • key：过滤器键名。
    • error_rate：错误率。错误率越低，所需空间越大。对于非精确场合可设置较大值。
    • capacity：预计放入的元素数量。当实际数量超出这个数值时，误判率会上升。该值估计的过大，会浪费存储空间，估计的过小，就会影响准确率。
  • 使用布隆过滤器时不要让实际元素远大于初始化大小，超出时应重建过滤器、分配更大 size 的过滤器，并导入所有历史元素 (需提前在外部保存历史元素)。
  • error_rate 不会因溢出而剧增，故重建过滤器的时间较为宽松，但也应提前合理设置。
  • 爬虫系统中过滤爬虫的 URL 非常适合使用布隆过滤器来统计，进而大幅降低去重存储消耗。
  • 布隆过滤器可以显著降低 DB 的 IO 请求数，在 NoSQL DB 领域使用广泛。
  • 垃圾邮件过滤功能也普遍用到了布隆过滤器，故正常邮件会被误判。
  • 用于计算布隆过滤器最佳参数的布隆计算器

延伸阅读：

updatedupdated2023-09-272023-09-27

相关文章：